A. Vasya and Coins
题意:
小明有a枚1元硬币和b枚2元硬币,输出小明无法支付的最小金额。
思路:
- 没有1元硬币:
答案为1
- 有1元硬币:
答案为a+2∗b+1
时间复杂度:
O(1)
AC代码:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
| 在这里插入代码片#include<bits/stdc++.h>
typedef long long ll;
const int N = 20,M = 2e4+10,INF = 0x3f3f3f3f,mod = 1e9+7;
void solve()
{
int a,b;
std::cin>>a>>b;
if(!a)
{
std::cout<<1<<'\n';
return;
}
std::cout<<a+b*2+1<<'\n';
}
int main()
{
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
std::cout.tie(nullptr);
int T;
std::cin>>T;
while(T--)
{
solve();
}
return 0;
}
|
B. Vlad and Candies
题意:
有n种糖果,每个糖果有ai份。
每次都吃掉份数最多的糖果,但是小明不希望连续两次吃一样的糖果,他是否可以按照这个要求吃掉所有糖果。
思路:
只需要考虑最大值和次大值即可。
最大值−次大值>1:NO
最大值−次大值≤1:YES
时间复杂度:
O(n)
AC代码:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
| #include<bits/stdc++.h>
typedef long long ll;
const int N = 20,M = 2e4+10,INF = 0x3f3f3f3f,mod = 1e9+7;
void solve()
{
int max1 = 0,max2 = 0;
int n;
std::cin>>n;
for(int i = 1 ; i <= n ; i++)
{
int x;
std::cin>>x;
if(x > max1)std::swap(max1,x);
if(x > max2)std::swap(max2,x);
}
std::cout<<(max1-max2 > 1 ?"NO":"YES")<<'\n';
}
int main()
{
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
std::cout.tie(nullptr);
int T;
std::cin>>T;
while(T--)
{
solve();
}
return 0;
}
|
C. Get an Even String
题意:
给定一个字符串S,要求你删除最少的字母,让字符串S满足如下要求:
- 长度为偶数
- ai=ai+1(i为奇数)
思路:
很显然,我们要把相同的字母匹配起来。
我们考虑如下贪心策略:
形如测试案例:bmefbmuyw
- 删除字母最少,就是保留字母最多
- 我们把上述字符串中,最近的匹配字母取出,组成区间
- 有[1,5],[2,6]
- 即在这些区间中,找到尽可能多的不相交区间。
- 而选择的标准就是右端点越小,那么选择一定是越好的,因为右端点越小,后面可供选择的区间一定会更多。
所以实际操作过程中,每当存在一对可以匹配的字母,我们就匹配他们,并把他们中间的字母全部删除(让右端点尽可能小)。
时间复杂度:
使用了map去存字母,所以时间复杂度增加logn
O(nlogn)
AC代码:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
| #include<bits/stdc++.h>
typedef long long ll;
const int N = 20,M = 2e4+10,INF = 0x3f3f3f3f,mod = 1e9+7;
void solve()
{
std::map<char,bool> mp;
std::string s;
std::cin>>s;
int res = 0;
for(int i = 0 ; i < s.size() ; i++)
{
if(mp.count(s[i]))
{
res += 2;
mp.clear();
}
else mp[s[i]] = true;
}
std::cout<<s.size() - res << '\n';
}
int main()
{
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
std::cout.tie(nullptr);
int T;
std::cin>>T;
while(T--)
{
solve();
}
return 0;
}
|
D. Maximum Product Strikes Back
题意:
给定长度为n的数组,而且其中的每一个元素∣ai∣≤2。
要求从右和从左删除一定个数的元素,使得剩下元素相乘之积最大:
选择x和y
求max∏i=xn−yai
思路:
因为空数组是1,所以0是必然被删除的,所以0把整个数组划分成了若干个区间,我们对每个这样的区间求取最大值,对每个区间,我们做这样的处理:
- 区间的值应该保持为正数
- 我们记录区间中负数的个数和2的个数
- 2的个数决定乘积大小,负数个数决定乘积是否为负。
- 在乘积已经是正数的基础上,那么区间的数留下的越多肯定是越好的。
- 区间内负数个数为偶数:
直接把当前区间乘积最为备选答案,与此时的答案相比。
- 区间内负数个数为奇数:
分别从左和从右寻找第一个负数,取两者更优的情况。
时间复杂度:
O(n)
AC代码:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
| #include<bits/stdc++.h>
typedef long long ll;
const int N = 2e5+10,M = 2e4+10,INF = 0x3f3f3f3f,mod = 1e9+7;
int a[N];
void solve()
{
int n;
int cnt_two = 0,cnt_negative = 0,ans = 0,last = 0;
std::pair<int,int> res;
std::cin>>n;
for(int i = 1 ; i <= n ; i++)std::cin>>a[i];
for(int i = 1 ; i <= n + 1; i++)
{
if(a[i] == 0||i == n + 1)
{
int t = 0;
if(cnt_negative&1)
{
for(int j = last + 1 ; j < i ; j++)
{
if(a[j] == 2||a[j] == -2)t++;
if(a[j] < 0)
{
if(cnt_two - t > ans)
{
ans = cnt_two - t;
res = {j, n + 1 - i};
}
break;
}
}
t = 0;
for(int j = i - 1; j > last ; j--)
{
if(a[j] == 2||a[j] == -2)t++;
if(a[j] < 0)
{
if(cnt_two - t > ans)
{
ans = cnt_two - t;
res = {last,n + 1 - j};
}
break;
}
}
}
else
{
if(cnt_two > ans)
{
ans = cnt_two;
res = {last,n + 1 - i};
}
}
last = i;
cnt_negative = cnt_two = 0;
}
else
{
if(a[i] == 2)cnt_two++;
else if(a[i]==-2)cnt_two++,cnt_negative++;
else if(a[i]==-1)cnt_negative++;
}
}
if(ans == 0)std::cout<<n<<" "<<0<<'\n';
else std::cout<<res.first<<" "<<res.second<<'\n';
}
int main()
{
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
std::cout.tie(nullptr);
int T;
std::cin>>T;
while(T--)
{
solve();
}
return 0;
}
|
E. Matrix and Shifts
题意:
有一个n∗n的矩阵,里面的每个元素都是0和1,可以任意执行以下4种操作(无需任何代价):
- 全体上移一行(第一行到最后一行)
- 全体下移一行(最后行到第一行)
- 全体左移一行(最左边一行到最右边一行)
- 全体右移一行(最右边一行到最左边一行)
操作完后,我们可以花费一个代价,执行这样的操作:
把某个元素从0变成1,或者从1变成0。
要求变完以后,只有对角线元素是1,其余均是0。
输出最小代价。
思路:
我们只要让尽可能多的1落在对角线上就可以了。
即以如下方式遍历矩阵:
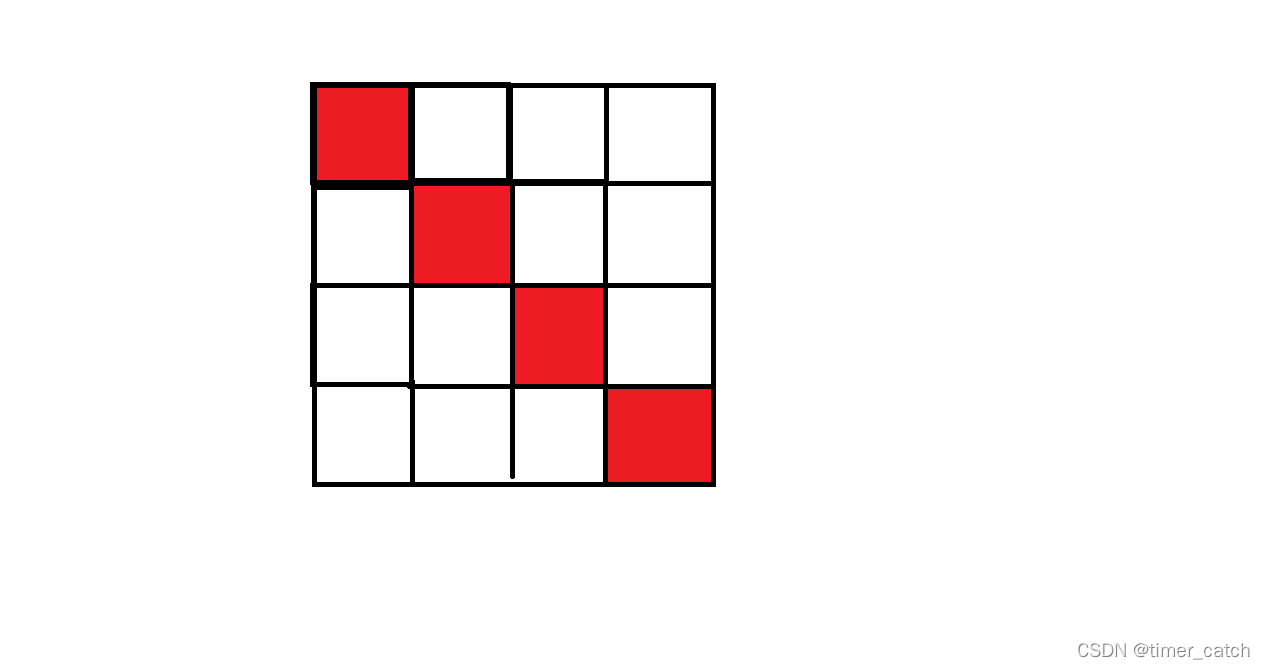
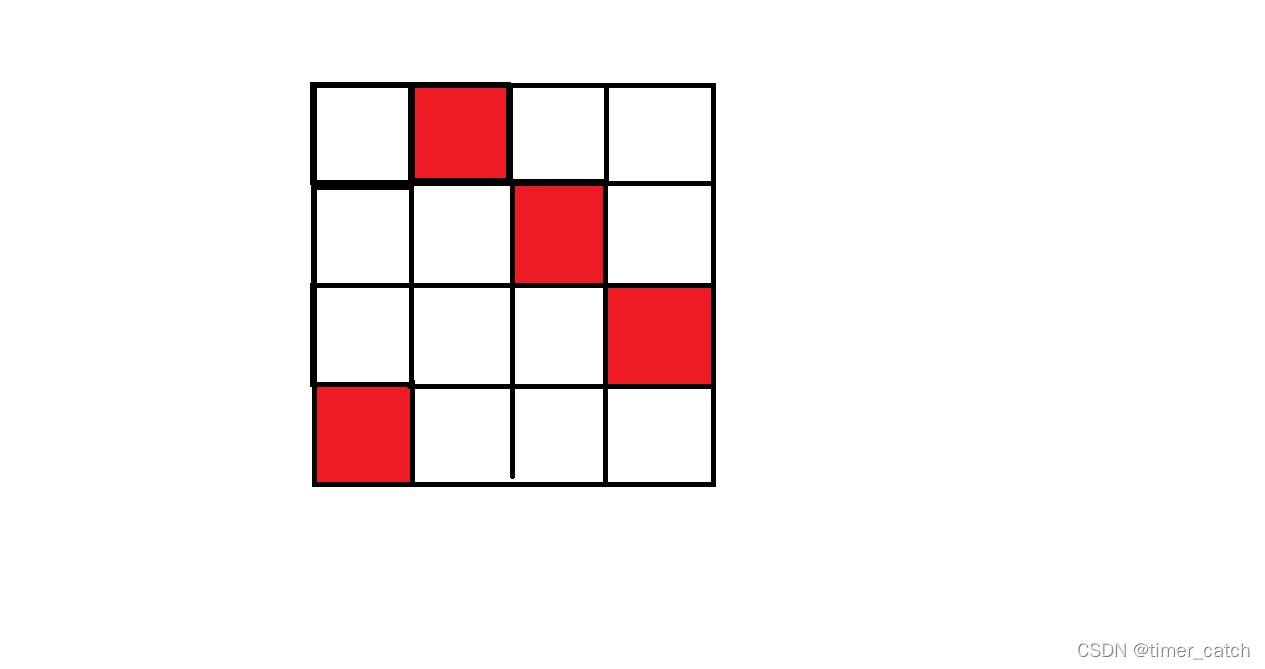
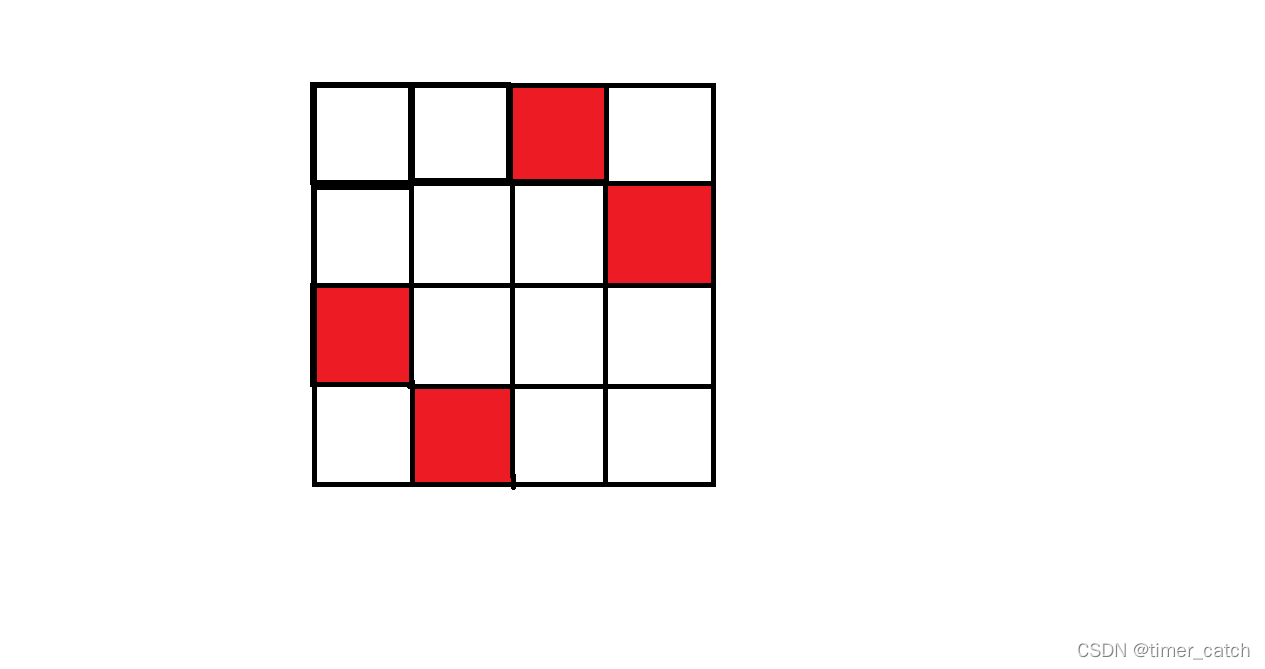
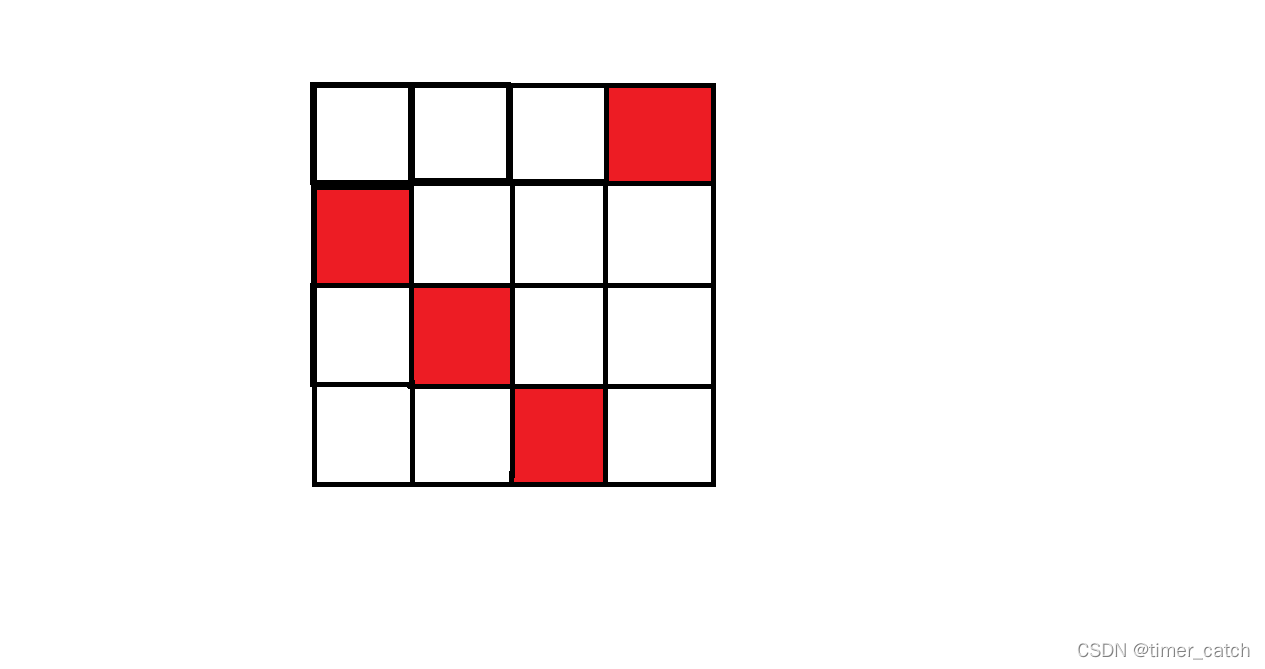
记录下 1 最多的数量 max。
那么最后要修改的数量就是:
- 在对角线上的 0 元素(n−max)
- 不在对角线上的 1 元素(cnt−max)
记录矩阵中 1 的个数为cnt:
所以最终答案为(n−max)+(cnt−max)
时间复杂度:
O(n2)
AC代码:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
| #include<bits/stdc++.h>
typedef long long ll;
const int N = 2e3+10,M = 2e4+10,INF = 0x3f3f3f3f,mod = 1e9+7;
int a[N][N];
void solve()
{
int n,cnt = 0,max = 0;
std::cin>>n;
for(int i = 1 ; i <= n ; i++)
{
std::string s;
std::cin>>s;
for(int j = 1 ; j <= n ; j++)
{
a[i][j] = s[j-1] - '0';
cnt += (a[i][j] == 1);
}
}
for(int j = 1 ; j <= n ; j++)
{
int y = j,temp = 0;
for(int i = 1 ; i <= n ; i++)
{
if(a[i][y] == 1)temp++;
y++;
if(y==n+1)y = 1;
}
max = std::max(max,temp);
}
std::cout<<cnt - max + (n - max)<<'\n';
}
int main()
{
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
std::cout.tie(nullptr);
int T;
std::cin>>T;
while(T--)
{
solve();
}
return 0;
}
|
F1. Promising String (easy version)
题意:
给定一个由’+'和‘-’组成的字符串S,定义有希望的字符串如下:
字符串可以进行如下操作:
相邻的两个’-‘可以合并为’+’
可以通过上述操作,使得字符串中’+'和‘-’的数量相同。
输出字符串S中所有满足条件的子串的个数。
思路:
因为数据量只有3000,所以我们直接暴力枚举所有区间。
检查区间合法的方法如下:
- 记录下区间中‘+‘的数量cnt1,‘-‘的数量cnt0,以及可以合并的减号的最大对数cnt。
- 假设合并的减号对数为x:
cnt0−2∗x=cnt1+x
cnt0−cnt1=3∗x
那么只需要满足x为整数,而且x≤cnt,区间就是合法的。
时间复杂度:
O(n2)
AC代码:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
| #include<bits/stdc++.h>
typedef long long ll;
const int N = 2e3+10,M = 2e4+10,INF = 0x3f3f3f3f,mod = 1e9+7;
void solve()
{
int n;
std::cin>>n;
std::string s;
std::cin>>s;
bool tag = false;
int cnt1,cnt0,cnt,res = 0;
for(int i = 0 ; i < n ; i++)
{
cnt = 0,cnt1 = 0,cnt0 = 0;
for(int j = i ; j < n ; j++)
{
if(s[j] == '+')cnt1++,tag = false;
else
{
if(tag)
{
cnt++;
cnt0++;
tag = false;
}
else
{
cnt0++;
tag = true;
}
}
if(cnt0==cnt1)res++;
else
{
if(cnt0 > cnt1 && (cnt0 - cnt1) % 3 == 0)
{
if(cnt >= (cnt0 - cnt1)/3 )res++;
}
}
}
}
std::cout<<res<<'\n';
}
int main()
{
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
std::cout.tie(nullptr);
int T;
std::cin>>T;
while(T--)
{
solve();
}
return 0;
}
|










